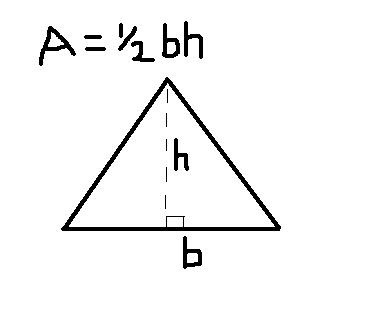
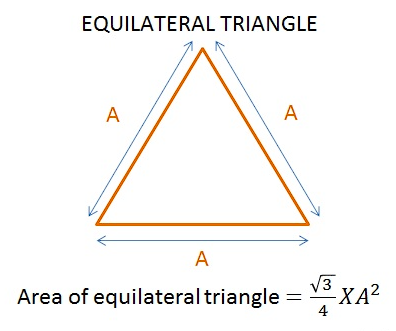
The area of a triangle is a foundational concept in geometry, enabling us to understand its spatial extent. For any triangle, the area (A) is calculated by multiplying the base (b) of the triangle by its corresponding height (h) and then dividing by 2, represented as the formula A = (b × h) / 2. This versatile formula applies to triangles of all types. However, when dealing with the elegant symmetry of an equilateral triangle, which boasts three equal sides and angles, a distinct formula emerges: A = (side length, a)² * (√3) / 4. This specialized equation showcases the unique characteristics of equilateral triangles, where the area is determined by the square of one side length (a) multiplied by the square root of 3 and then divided by 4, emphasizing the symmetrical allure that sets equilateral triangles apart in the realm of geometry.